Mapeando sobre un pangenoma de arroz con minigraph

Hola,

hace unos meses contruí un pangenoma a partir de 15 genomas de arroz obtenidos de Ensembl Plants. Para ello he probado el software minigraph, descrito en https://doi.org/10.1186/s13059-020-02168-z , que es una de las herramientas disponibles para construir un grafo genómico, en este caso por medio de inserciones y deleciones sobre el genoma de referencia (naranja en la figura).

 

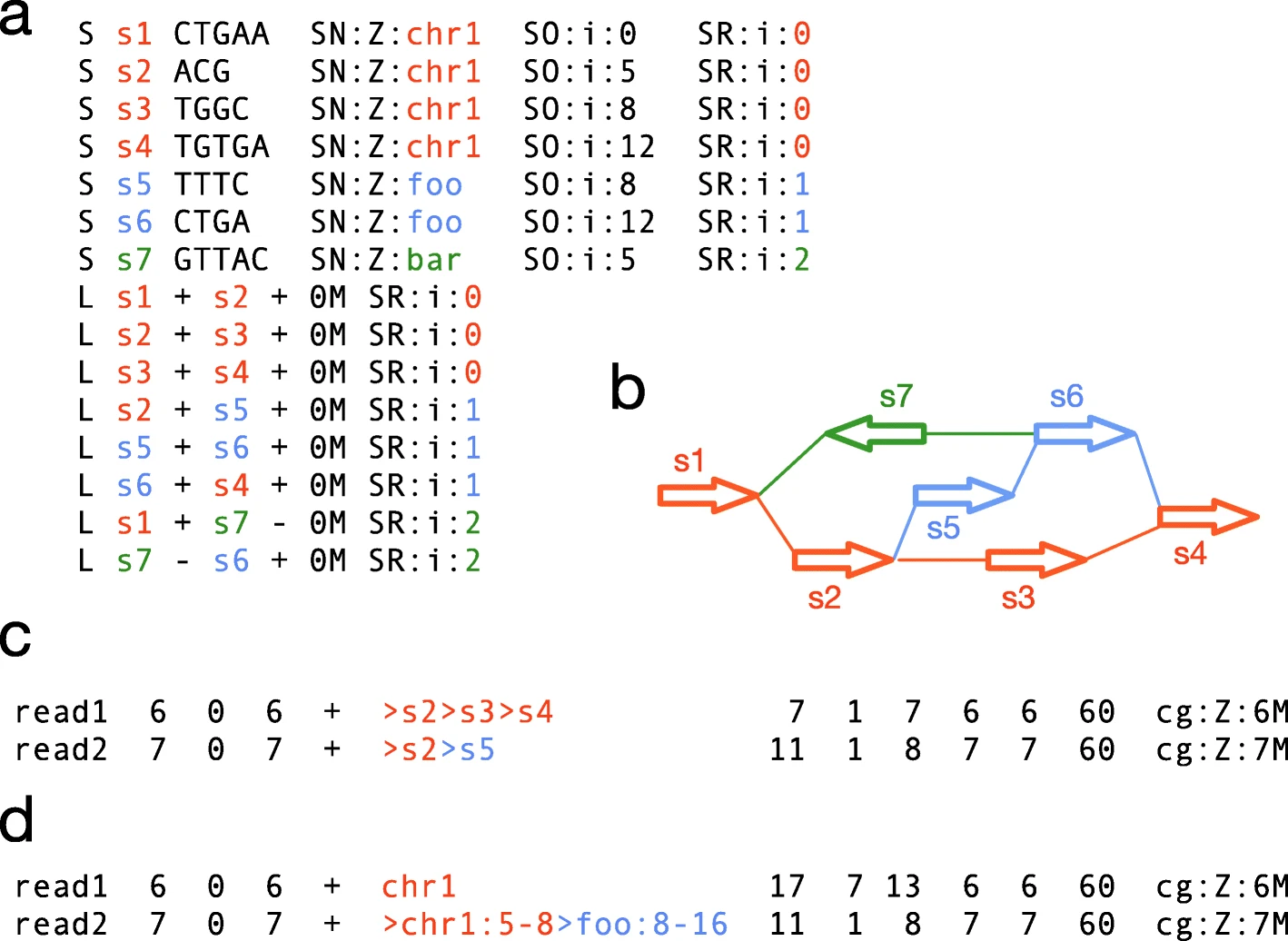Figura. Mapeo de lecturas sobre un grafo pangenómico, figura tomada de https://doi.org/10.1186/s13059-020-02168-z

Hoy quería resumir aquí cómo se hace por si le ayuda a alguien.

El primer paso es construir el grafo a partir de varios genomas individuales, de arroz en este caso. Para ello deberás partir de ficheros FASTA donde cada cromosoma tenga un nombre único. Eso se puede lograr por ejemplo agregando al nombre de cromosoma original el identificador o accession de cada genoma:

# 1) prepare genome FASTA files, making sure chr names are unique
mkdir fasta
while read core; do 
	echo $core; 
	perl -lne 'BEGIN{ if($ARGV[0] =~ /sativa_([^_]+)/){ $acc=$1 }} if(/^>(\S+)/){ print ">$1_$acc" } else {print}' ${acc}.fna > ${acc}.uniq.fna 
done < ../liftover/list_cores.txt

# build the graph
bsub -M 40G -n 10 -cwd soft/minigraph/minigraph -xggs -t 10 oryza_sativa_core_48_101_7.fna fasta/*.fna -o oryza_sativa.gfa

Este proceso genera la siguiente salida:

[M::main::0.702*0.84] loaded the graph from "oryza_sativa_core_48_101_7.fna"
[M::mg_index::9.913*1.50] indexed the graph
[M::mg_opt_update::10.576*1.47] occ_weight=20, occ_max1=178; 95 percentile: 2
[M::ggen_map::11.491*1.42] loaded file "fasta/oryza_sativa_Azucena_core_48_101_1.fna"
[M::ggen_map::168.948*6.05] mapped 37 sequence(s) to the graph
[M::mg_ggsimple::170.379*6.01] inserted 15028 events, including 39 inversions
[M::mg_index::180.913*5.75] indexed the graph
...
[M::main] Real time: 13152.427 sec; CPU: 82007.142 sec; Peak RSS: 47.687 GB

Ahora podemos probar a mapear secuencias de cDNA sobre el grafo:

# read
https://twitter.com/zhigui_bao/status/1417028758725222400
https://github.com/lh3/minigraph/issues/37

# Note in rice -N 0 /-N 100 made no difference!
soft/minigraph/minigraph -t 4 -j 0.02 oryza_sativa.gfa -N 100 \
	oryza_nivara.cdna.fna | sort -k1,1 -k10,10nr > Onivara.cdna.graph.sort.gaf
soft/minigraph/minigraph -t 4 -j 0.02 oryza_sativa.gfa -N 100 \
	oryza_sativa.cdna.fna | sort -k1,1 -k10,10nr > Osativa.cdna.graph.sort.gaf
soft/minigraph/minigraph -t 4 -j 0.02 oryza_sativa.gfa -N 100 \
	oryza_indica.cdna.fna | sort -k1,1 -k10,10nr > Oindica.cdna.graph.sort.gaf

Hasta pronto, Bruno

grafos de De Bruijn

Hola,
un artículo educativo publicado recientemente en Nature Biotechnology me ha vuelto a recordar los grafos de De Bruijn, que ya había mencionado de pasada en una entrada anterior sobre vectores de sufijos. Hoy los veremos un poco más de cerca, por su importancia para la reconstrucción de secuencias genómicas a partir de fragmentos más pequeños que han sido previamente secuenciados.

Los modernos ensambladores de secuencias emplean grafos de De Bruijn para guardar en memoria los prefijos (nodos) y sufijos (aristas) de las lecturas o reads obtenidas en experimentos de secuenciación. Este tipo de representación permite reducir en parte la redundancia natural de este tipo de datos a la vez que facilita su ensamblaje posterior. La figura  compara los métodos de ensamblaje tradicionales (a) con los actuales (d). Los tradicionales se usan para pegar entre si secuencias obtenidas por el método de Sanger, que suelen ser largas, de buena calidad y en números pequeños. Los métodos que acompañan a los secuenciadores actuales se adaptan al nuevo escenario de secuencias cortas y en números varios órdenes de magnitud más elevados.

fuente: http://www.nature.com/nbt/journal/v29/n11/full/nbt.2023.html

Como se muestra en el panel d de la figura, un grafo de De Bruijn facilita la reconstrucción del genoma de partida, que se obtiene buscando un ciclo euleriano que recorra todas las aristas (sufijos) una sola vez. Esta estrategia es computacionalmente mucho más barata que la alternativa de buscar ciclos hamiltonianos, que en la práctica es imposible al ser un problema de tipo NP completo. Sin embargo, como pasa a menudo, la realidad se resiste a ser capturada por una sola teoría, e incluso los grafos de De Bruijn son todavía incapaces de resolver el problema de las secuencias repetidas, que aparecen en un genoma o región genómica no una sinó muchas veces.

En el Russell's blog encontraréis código fuente en Python para aprender cómo se construyen estos grafos. Espero haberos despertado la curiosidad, un saludo,
Bruno